↧
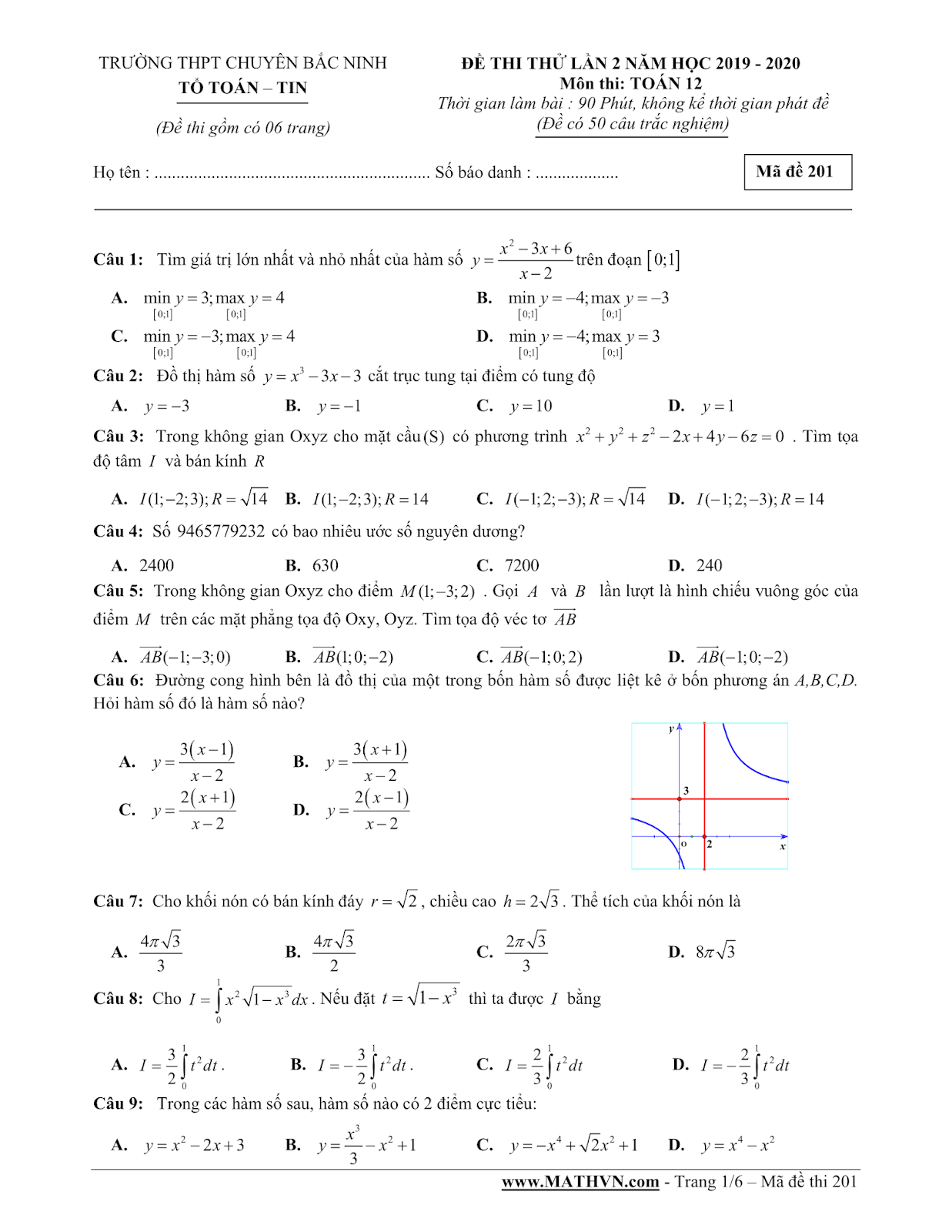
File word đề thi thử môn Toán năm 2020 trường chuyên Bắc Ninh có đáp án
Đề thi thử đại học ( thi thpt quốc gia ) môn Toán lần 2 năm 2020 trường chuyên Bắc Ninh. Kì thi vừa diễn ra vào tuần này. Đề gồm 50 câu trắc nghiệm Toán có đáp án. Đề được biên soạn theo mức độ và cấu trúc đề thi của Bộ Giáo dục những năm gần đây. Dưới đây là file ảnh, file PDF và file word của đề thi này.
TheoChuyên Bắc Ninh. Người đăng: Tố Uyên.
↧
Đề thi học sinh giỏi Quốc gia môn Toán năm 2020 - Ngày 1
Đề thi môn Toán trong kì thi chọn học sinh giỏi quốc gia môn Toán THPT, ngày thi thứ nhất, 27/12/2019.
Đề gồm 4 câu, mỗi câu 5 điểm. Thời gian làm bài 180 phút.
Dân chuyên Toán đặt tên cho kì thi này là VMO 2020.
Thí sinh không được sử dụng máy tính cầm tay trong phòng thi.
Các thí sinh sẽ tiếp tục thi ngày thứ 2 vào sáng mai, 28/12.
Xem thêm:Lời giải đề VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
Đề gồm 4 câu, mỗi câu 5 điểm. Thời gian làm bài 180 phút.
Dân chuyên Toán đặt tên cho kì thi này là VMO 2020.
Thí sinh không được sử dụng máy tính cầm tay trong phòng thi.
Các thí sinh sẽ tiếp tục thi ngày thứ 2 vào sáng mai, 28/12.
TheoVMO. Người đăng: Tố Uyên.
Xem thêm:Lời giải đề VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
↧
↧
Lời giải bài bất đẳng thức trong đề VMO 2020 - Ngày 1 (Bài 2)
Xin giới thiệu Lời giải bài bất đẳng thức (Câu 2) trong đề VMO 2020 - Ngày 1 của kì thi chọn học sinh giỏi quốc gia môn Toán THPT năm học 2019 - 2020. Buổi thi đầu tiên vừa diễn ra vào sáng nay 27/12.
Lời giải của tác giả Võ Quốc Bá Cẩn - một chuyên gia bất đẳng thức nổi tiếng của Việt Nam - người đang giảng dạy ở Hà Nội.
Theo thầy Cẩn, đây là một bài toán hay với ý tưởng nhẹ nhàng, trong sáng. Dạng bài này cũng đã xuất hiện trước đó. Có lẽ, tác giả bài toán đã lấy ý tưởng bài này từ đề chọn đội tuyển Romania 2008.
Xem thêm:Lời giải VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
Lời giải của tác giả Võ Quốc Bá Cẩn - một chuyên gia bất đẳng thức nổi tiếng của Việt Nam - người đang giảng dạy ở Hà Nội.
Theo thầy Cẩn, đây là một bài toán hay với ý tưởng nhẹ nhàng, trong sáng. Dạng bài này cũng đã xuất hiện trước đó. Có lẽ, tác giả bài toán đã lấy ý tưởng bài này từ đề chọn đội tuyển Romania 2008.
TheoVõ Quốc Bá Cẩn. Người đăng: Dịu.
Xem thêm:Lời giải VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
↧
Lời giải câu Số học trong đề VMO 2020 - Ngày 1 (Bài 3)
Bài 3 (VMO 2020 - Day 1) trong đề chọn học sinh giỏi quốc gia môn Toán năm 2020 là một câu thuộc lĩnh vực Số học. Bài viết này giới thiệu 2 lời giải của bài toán này.
Xem thêm:Lời giải VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
Đề bài toán Số học ở VMO 2020 - Ngày 1
Lời giải 1 - Tác giả: Nguyễn Song Minh
Lời giải 2 - Tác giả: Võ Quốc Bá Cẩn
TheoNguyễn Song Minh, Võ Quốc Bá Cẩn. Người đăng: Dịu.
Xem thêm:Lời giải VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
↧
Lời giải câu Hình học trong đề học sinh giỏi quốc gia 2020 ngày 1 (Bài 4)
Xin giới thiệu hai lời giải câu Hình học (bài 4) trong đề thi chọn học sinh giỏi quốc gia môn Toán 2020 ngày 1 - VMO 2020 Day 1. Hai lời giải của 2 tác giả: Nguyễn Văn Linh và Trịnh Huy Vũ.
Bài 4a)
Bài 4b)
Bài 4a)
Bài 4b)
Xem thêm:Lời giải VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
 |
| Hình vẽ bài 4 của Nguyễn Văn Linh |
Đề bài 4 VMO 2020 ngày 1 (hình học)
LỜI GIẢI 1 - Tác giả: Nguyễn Văn Linh
Xem hình vẽ ở đầu bài.Bài 4a)
Bài 4b)
LỜI GIẢI 2 - Tác giả: Trịnh Huy Vũ
Hình vẽ |
| Hình vẽ bài 4 của tác giả Trịnh Huy Vũ |
Bài 4b)
TheoNguyễn Văn Linh, Trịnh Huy Vũ. Người đăng: Dịu.
Xem thêm:Lời giải VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
↧
↧
Lời giải câu Giới hạn dãy số trong đề VMO 2020 (Bài 1)
Lời giải câu Giới hạn dãy số trong đề VMO 2020 (Bài 1) - kì thi chọn học sinh giỏi quốc gia môn Toán THPT năm học 2019 - 2020, vừa diễn ra sáng nay 27/12. Đề thi đã được đăng trong bài viết trước. Dưới đây là lời giải chi tiết bài 1.
Thật vậy, với $n=1$ thì bất đẳng thức hiển nhiên đúng. Giả sử bất đẳng thức đúng với $n=k \geq 1.$
Với $n=k+1$ ta có $$x_{k+1} \geq x_k + 3\sqrt{x_k} \geq k^2+3k \geq (k+1)^2.$$
Vậy $$0<\frac{n}{x_n} \leq \frac{n}{n^2}=\frac{1}{n}, \forall n \geq 1.$$
Suy ra điều phải chứng minh.
Xem thêm:Lời giải VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
Đề bài 1 VMO 2020 (Dãy số)
Lời giải câu 1a
Ta sẽ chứng minh $$x_n \geq n^2, \forall n \geq 1.$$Thật vậy, với $n=1$ thì bất đẳng thức hiển nhiên đúng. Giả sử bất đẳng thức đúng với $n=k \geq 1.$
Với $n=k+1$ ta có $$x_{k+1} \geq x_k + 3\sqrt{x_k} \geq k^2+3k \geq (k+1)^2.$$
Vậy $$0<\frac{n}{x_n} \leq \frac{n}{n^2}=\frac{1}{n}, \forall n \geq 1.$$
Suy ra điều phải chứng minh.
Lời giải câu 1b
Lời giải câu 1b của tác giả Võ Quốc Bá Cẩn.TheoVõ Quốc Bá Cẩn. Người đăng: Dịu.
Xem thêm:Lời giải VMO 2020 Ngày 1: Bài 1 - Bài 2 - Bài 3 - Bài 4.
↧
Đề thi HSG Quốc gia 2020 môn Toán ngày 2 - VMO 2020 Day 2
Sáng 28/12/2019, học sinh giỏi Toán toàn quốc bước vào ngày thi thứ 2 của kì thi chọn HSG quốc gia môn Toán năm 2020 (viết tắt là VMO 2020 - Day 2).
Dưới đây là đề thi môn Toán. Đề ngày 2 gồm 3 câu về các lĩnh vực: Đại số, Hình học và Tổ hợp.
Tổng điểm bài thi Toán ngày 2 vẫn là 20 điểm như ngày 1. Thời gian làm bài 180 phút.
Thí sinh không được sử dụng máy tính cầm tay.
Xem lại: Đề VMO 2020 ngày 1 và lời giải.
Dưới đây là đề thi môn Toán. Đề ngày 2 gồm 3 câu về các lĩnh vực: Đại số, Hình học và Tổ hợp.
Tổng điểm bài thi Toán ngày 2 vẫn là 20 điểm như ngày 1. Thời gian làm bài 180 phút.
Đề Toán chọn học sinh giỏi quốc gia năm 2020
Ngày thi thứ hai: 28/12/2019.Thí sinh không được sử dụng máy tính cầm tay.
Lời giải đề VMO 2020 Ngày 2
TheoVMO 2020. Người đăng: Sơn Phan.
Xem lại: Đề VMO 2020 ngày 1 và lời giải.
↧
Lời giải Bài 6 (Hình học) trong đề VMO 2020 - Ngày 2
Bài hình học ở ngày thi thứ hai của kì thi chọn học sinh giỏi quốc gia môn Toán THPT năm 2020 (VMO 2020 Day 2) được đánh giá là nhẹ hơn so với bài hình của ngày thi thứ nhất.
Dưới đây là đề bài và lời giải câu hình học VMO 2020 Ngày 2 của tác giả Nguyễn Văn Linh.
| Hình vẽ Bài 6 đề VMO 2020 |
Đề bài hình học ngày 2 VMO 2020 (Bài 6)
Lời giải Bài 6 VMO 2020 ngày 2
Tác giả lời giải cũng nhận xét rằng bài 6 này khá nhẹ nhàng.TheoNguyễn Văn Linh. Người đăng: Sơn Phan.
↧
Lời giải câu Hệ phương trình trong đề VMO 2020 (Bài 5)
Giới thiệu lời giải câu Hệ phương trình trong đề VMO 2020 ngày thứ 2 (Bài 5). Lời giải của tác giả Lê Phúc Lữ với 2 cách khác nhau cho câu 5b.
Xem thêm:Giải đề VMO 2020 ngày 2: Lời giải Bài 5 (Hệ phương trình) - Lời giải Bài 6 (Hình học) - Lời giải Bài 7 (Tổ hợp).
Đề bài 5 VMO 2020 - Hệ phương trình
Ý a) ở mức độ vừa phải. Ý b) đòi hỏi thí sinh phải chắc tay mới xử lí gọn gàng và chặt chẽ được.Lời giải bài 5a
Lời giải bài 5b - Cách 1
Lời giải bài 5b - Cách 2
Nhận xét. Ở bài toán này, ý a có thể nói là không thể không làm được. Tuy nhiên, ý b lại đòi hỏi phải tính toán khá chắc tay. Nếu ta biến đổi rút các biến thế “chồng chéo” vào nhau rồi đưa về một phương trình bậc cao rất khó để chỉ ra nó có đủ 5 nghiệm. Ý tưởng đối xứng hóa ở đây cũng tương đối tự nhiên. Đây là một bài đại số ứng dụng đa thức rất mới mẻ và thú vị.TheoLê Phúc Lữ. Người đăng: Sơn Phan.
Xem thêm:Giải đề VMO 2020 ngày 2: Lời giải Bài 5 (Hệ phương trình) - Lời giải Bài 6 (Hình học) - Lời giải Bài 7 (Tổ hợp).
↧
↧
Lời giải bài Tổ hợp đề thi VMO 2020 ngày 2 (Bài 7)
Xin giới thiệu Lời giải bài Tổ hợp đề thi VMO 2020 ngày 2 (Bài 7 - kì thi chọn học sinh giỏi quốc gia năm 2020) của tác giả Lê Phúc Lữ.
b) Chứng minh rằng tồn tại một tập hợp liên kết với T có đúng 2n(n−1) phần tử.
c) Chứng minh rằng mỗi tập hợp liên kết với T có không ít hơn 2n(n−1) phần tử.
Xem thêm:Giải đề VMO 2020 ngày 2: Lời giải Bài 5 (Hệ phương trình) - Lời giải Bài 6 (Hình học) - Lời giải Bài 7 (Tổ hợp).
Đề bài 7 - VMO 2020 ngày 2
a) Tính số phần tử của T.b) Chứng minh rằng tồn tại một tập hợp liên kết với T có đúng 2n(n−1) phần tử.
c) Chứng minh rằng mỗi tập hợp liên kết với T có không ít hơn 2n(n−1) phần tử.
Lời giải bài 7 (tổ hợp) VMO 2020
Nhận xét. Bài toán này thực ra là một cách phát biểu của khéo léo, che giấu đi bản chất vấn đề của định lý Mantel – Turan. Quan hệ “không có tam giác” phát biểu thông qua ràng buộc khá rõ, nhưng cần phải xử lý cẩn thận, vì đề cho quan hệ có hướng (trong khi định lý chỉ áp dụng được cho graph vô hướng).TheoLê Phúc Lữ. Người đăng: Sơn Phan.
Xem thêm:Giải đề VMO 2020 ngày 2: Lời giải Bài 5 (Hệ phương trình) - Lời giải Bài 6 (Hình học) - Lời giải Bài 7 (Tổ hợp).
↧
Một cách giải khác cho câu bất đẳng thức trong đề VMO 2020
Bài viết trước đã giới thiệu lời giải câu bất đẳng thức trong đề thi chọn học sinh giỏi quốc gia môn Toán năm 2020 (Bài 2b đề VMO 2020 Ngày 1).
Bài này giới thiệu một cách giải khác của tác giả Lê Phúc Lữ cho câu bất đẳng thức này.
Xem lại toàn bộ đề thi học sinh giỏi quốc gia môn Toán 2020: Ngày 1 - Ngày 2
Bài này giới thiệu một cách giải khác của tác giả Lê Phúc Lữ cho câu bất đẳng thức này.
Nhắc lại đề bài bất đẳng thức
Một lời giải khác cho câu 2b
Cách giải này được đánh giá là gọn gàng và mạch lạc hơn cách trước.TheoLê Phúc Lữ. Người đăng: Sơn Phan.
Xem lại toàn bộ đề thi học sinh giỏi quốc gia môn Toán 2020: Ngày 1 - Ngày 2
↧
Câu hỏi Toán trong Đường lên đỉnh Olympia năm thứ 20 - Phần 5
Bài viết này tiếp tục giới thiệu các câu hỏi Toán trong chương trình Đường lên đỉnh Olympia năm thứ 20 phát sóng ngày 29/12/2019 trên VTV3, cuộc thi tuần 2, tháng 1, quý II.
Câu 2. Dùng compa để vẽ đường gì?
Câu 3. Bây giờ là mấy giờ?
Câu 4. Tính số sách quyên góp của mỗi lớp?
Câu 5. Tính quãng đường.
Câu 1. 53 độ.
Câu 2. Đường tròn.
Câu 3. 7 giờ 30 phút.
Câu 4. 480 - 640 - 800
Câu 5. 5 km.
Đề bài 5 câu hỏi Toán
Câu 1. Tính số đo góc được tô màu vàng.Câu 2. Dùng compa để vẽ đường gì?
Câu 3. Bây giờ là mấy giờ?
Câu 4. Tính số sách quyên góp của mỗi lớp?
Câu 5. Tính quãng đường.
Đáp án 5 câu hỏi Toán OLP20 - 29/12/2019
Câu 1. 53 độ.
Câu 2. Đường tròn.
Câu 3. 7 giờ 30 phút.
Câu 4. 480 - 640 - 800
Câu 5. 5 km.
ẢnhVTV. Người đăng: Tố Uyên Trần.
↧
Nhận xét và bình luận đề thi học sinh giỏi quốc gia môn Toán năm 2020
Kỳ thi chọn học sinh giỏi quốc gia môn Toán (viết tắt là VMO) năm 2020 diễn ra vào các ngày 27, 28 tháng 12/2019. Cấu trúc đề Toán năm nay là: 1. Giới hạn dãy số (Giải tích); 2. Bất đẳng thức (Đại số); 3. Dãy số nguyên (Số học); 4. Hình học phẳng (Hình học); 5. Hệ phương trình (Đại số); 6. Hình học phẳng (Hình học); 7. Tổ hợp.
Dưới đây là nhận xét và bình luận của thầy Lê Phúc Lữ - một chuyên gia luyện thi Olympic Toán của Việt Nam.
Tổng quan về đề thi, có thể nói đề ngày 1 so với "cùng kỳ năm trước" quả thật rất khác. Các câu hỏi đều có ý a để dẫn dắt gợi mở và thậm chí là cho điểm. Ý tưởng tuy không mới mẻ bằng năm trước nhưng cũng là các thử thách đáng kể với thí sinh. Hầu hết các thí sinh nếu ôn luyện cẩn thận sẽ làm tốt 4 ý a, và có thể làm thêm 1 ý b nào đó nữa. Các ý b có độ khó cũng khá tương đương nhau, tùy vào sở trường của thí sinh, nhưng nhìn chung số bạn làm được trọn vẹn cả bài hình là không nhiều.
Ngày thi thứ hai có một bất ngờ lớn khi xuất hiện câu biện luận hệ phương trình cũng như ý tổ hợp a quá nhẹ nhàng. Các câu hệ a và tổ a xem như cho điểm hoàn toàn. Cả câu hình và tổ b cũng ở mức trung bình (xây dựng mô hình khá đơn giản). Tuy nhiên, câu hệ b và tổ c quả thực là thách thức lớn, đòi hỏi phải kỹ năng xử lý tình huống tốt.
Nhìn chung, đề thi năm nay mới mẻ, đòi hỏi thí sinh vừa phải nắm chắc kiến thức, vừa phải có ít nhiều sáng tạo mới có thể làm trọn vẹn được.
Bài 1. Một bài về giới hạn dãy số truy hồi, có dùng định lý kẹp, định lí trung bình Cesaro hoặc định lí Stolz để giải quyết. Câu b hơi khó nhằn nhưng với sự gợi ý từ câu a, học sinh nắm chắc giới hạn có thể xử lý được.
Câu b có thể sử dụng định lý Stolz cho dãy (a_n) và dãy z_n = n cũng thu được kết quả tương tự, vì thực ra định lý Stolz còn tổng quát hơn cả định lý trung bình Cesaro. Dấu hiệu nhận biết định lý Stolz cho câu b là khá rõ.
Xem lại đề bài 1 và lời giải.
Bài 2. Một bài bất đẳng thức. Câu a dễ và gần như cho điểm các thí sinh. Nó còn là một gợi ý hiệu quả khi giải câu b. Nếu thay câu a gốc thành bài toán tìm GTLN ứng với 2020 số thì ta có thể thực hiện ngay BĐT Cauchy-Schwarz. Như thế thì bài toán này có thể đổi giả thiết từ 2019 lên n là số nguyên dương bất kỳ. Xét về bản chất của lời giải, ở trường hợp 2019 số, ta vẫn thực hiện được tương tự trên nhưng lại không thể chỉ ra dấu bằng theo kiểu ghép thành từng cặp đan dấu được.
Xem lại đề bài 2 và lời giải.
Bài 3. Một bài số học. Câu a là một kết quả nhẹ nhàng có thể thực hiện theo nhiều cách. Câu b là một bổ đề quen thuộc về cấp của một số liên quan đến số Fermat: Mỗi ước nguyên tố p của số 2^2^n + 1 thì đều thỏa mãn 2n+1|p − 1. Ta còn chứng minh được 2n+2|p − 1. Trên thực tế, cặp số (2, 1) ở trên có thể đổi thành cặp (a, b) nguyên tố cùng nhau bất kỳ. Và có lẽ ý tưởng này đã được khai thác để xây dựng thành bài toán trong đề thi.
Xem lại đề bài 3 và lời giải.
Bài 4. Bài hình học khó của toàn bộ đề thi. Khó hơn bài hình của ngày thứ hai (Bài 6). Bài toán này là khó nhất của ngày 1 và ý b đòi hỏi phải có các bước xử lý khá cầu kỳ mới phát hiện ra được điểm đồng quy thứ hai của ba đường tròn. Bài toán vẫn còn nhiều cách tiếp cận khác như dùng phép nghịch đảo. Theo tính bình đẳng giữa các đỉnh tam giác, ta thấy rằng L còn nằm trên đường tròn (BCD).
Xem lại đề bài 4 và lời giải.
Bài 5. Một câu hệ phương trình. Ở bài toán này, ý a có thể nói dễ và thí sinh không thể không làm được. Tuy nhiên, ý b lại đòi hỏi phải tính toán khá chắc tay. Nếu ta biến đổi rút các biến thế “chồng chéo” vào nhau rồi đưa về một phương trình bậc cao rất khó để chỉ ra nó có đủ 5 nghiệm. Ý tưởng đối xứng hóa ở đây cũng tương đối tự nhiên. Đây là một bài đại số ứng dụng đa thức rất mới mẻ và thú vị.
Xem lại đề bài 5 và lời giải.
Bài 6. Đây là bài hình học phẳng thứ hai của đề thi, và nó dễ hơn bài 4. Mô hình của bài toán khai thác khá mới mẻ nhưng không khó. Có nhiều cách tiếp cận để chứng minh ý b, theo kiểu tính toán hệ thức lượng hoặc biến đổi góc. Hướng xử lý theo kiểu dùng hàng điểm điều hòa như trên khá nhẹ nhàng và đẹp mắt. Nếu quan sát kỹ, ta thấy bản chất các điểm M, N chính là tiếp điểm của đường tròn bàng tiếp (A) của tam giác DEF lên các cạnh DE, DF. Ta còn chứng minh được DK, AX cùng đi qua điểm chung khác A của (I) và đường tròn đường kính AD.
Xem lại đề bài 6 và lời giải.
Bài 7. Một bài tổ hợp. Bài toán này thực ra là một cách phát biểu của khéo léo, che giấu đi bản chất vấn đề của định lý Mantel – Turan. Quan hệ “không có tam giác” phát biểu thông qua ràng buộc khá rõ, nhưng cần phải xử lý cẩn thận, vì đề cho quan hệ có hướng (trong khi định lý chỉ áp dụng được cho graph vô hướng). Trên thực tế, câu b chỉ là một cách xây dựng ví dụ cho dấu bằng xảy ra ở định lý này. Còn câu c có thể chứng minh trực tiếp bằng quy nạp.
Xem lại đề bài 7 và lời giải.
Dưới đây là nhận xét và bình luận của thầy Lê Phúc Lữ - một chuyên gia luyện thi Olympic Toán của Việt Nam.
Nhận xét tổng quan đề thi
Tổng quan về đề thi, có thể nói đề ngày 1 so với "cùng kỳ năm trước" quả thật rất khác. Các câu hỏi đều có ý a để dẫn dắt gợi mở và thậm chí là cho điểm. Ý tưởng tuy không mới mẻ bằng năm trước nhưng cũng là các thử thách đáng kể với thí sinh. Hầu hết các thí sinh nếu ôn luyện cẩn thận sẽ làm tốt 4 ý a, và có thể làm thêm 1 ý b nào đó nữa. Các ý b có độ khó cũng khá tương đương nhau, tùy vào sở trường của thí sinh, nhưng nhìn chung số bạn làm được trọn vẹn cả bài hình là không nhiều.
Ngày thi thứ hai có một bất ngờ lớn khi xuất hiện câu biện luận hệ phương trình cũng như ý tổ hợp a quá nhẹ nhàng. Các câu hệ a và tổ a xem như cho điểm hoàn toàn. Cả câu hình và tổ b cũng ở mức trung bình (xây dựng mô hình khá đơn giản). Tuy nhiên, câu hệ b và tổ c quả thực là thách thức lớn, đòi hỏi phải kỹ năng xử lý tình huống tốt.
Nhìn chung, đề thi năm nay mới mẻ, đòi hỏi thí sinh vừa phải nắm chắc kiến thức, vừa phải có ít nhiều sáng tạo mới có thể làm trọn vẹn được.
Nhận xét cụ thể từng bài
Ngày thi thứ nhất
Bài 1. Một bài về giới hạn dãy số truy hồi, có dùng định lý kẹp, định lí trung bình Cesaro hoặc định lí Stolz để giải quyết. Câu b hơi khó nhằn nhưng với sự gợi ý từ câu a, học sinh nắm chắc giới hạn có thể xử lý được.
Câu b có thể sử dụng định lý Stolz cho dãy (a_n) và dãy z_n = n cũng thu được kết quả tương tự, vì thực ra định lý Stolz còn tổng quát hơn cả định lý trung bình Cesaro. Dấu hiệu nhận biết định lý Stolz cho câu b là khá rõ.
Xem lại đề bài 1 và lời giải.
Bài 2. Một bài bất đẳng thức. Câu a dễ và gần như cho điểm các thí sinh. Nó còn là một gợi ý hiệu quả khi giải câu b. Nếu thay câu a gốc thành bài toán tìm GTLN ứng với 2020 số thì ta có thể thực hiện ngay BĐT Cauchy-Schwarz. Như thế thì bài toán này có thể đổi giả thiết từ 2019 lên n là số nguyên dương bất kỳ. Xét về bản chất của lời giải, ở trường hợp 2019 số, ta vẫn thực hiện được tương tự trên nhưng lại không thể chỉ ra dấu bằng theo kiểu ghép thành từng cặp đan dấu được.
Xem lại đề bài 2 và lời giải.
Bài 3. Một bài số học. Câu a là một kết quả nhẹ nhàng có thể thực hiện theo nhiều cách. Câu b là một bổ đề quen thuộc về cấp của một số liên quan đến số Fermat: Mỗi ước nguyên tố p của số 2^2^n + 1 thì đều thỏa mãn 2n+1|p − 1. Ta còn chứng minh được 2n+2|p − 1. Trên thực tế, cặp số (2, 1) ở trên có thể đổi thành cặp (a, b) nguyên tố cùng nhau bất kỳ. Và có lẽ ý tưởng này đã được khai thác để xây dựng thành bài toán trong đề thi.
Xem lại đề bài 3 và lời giải.
Bài 4. Bài hình học khó của toàn bộ đề thi. Khó hơn bài hình của ngày thứ hai (Bài 6). Bài toán này là khó nhất của ngày 1 và ý b đòi hỏi phải có các bước xử lý khá cầu kỳ mới phát hiện ra được điểm đồng quy thứ hai của ba đường tròn. Bài toán vẫn còn nhiều cách tiếp cận khác như dùng phép nghịch đảo. Theo tính bình đẳng giữa các đỉnh tam giác, ta thấy rằng L còn nằm trên đường tròn (BCD).
Xem lại đề bài 4 và lời giải.
Ngày thi thứ hai
Bài 5. Một câu hệ phương trình. Ở bài toán này, ý a có thể nói dễ và thí sinh không thể không làm được. Tuy nhiên, ý b lại đòi hỏi phải tính toán khá chắc tay. Nếu ta biến đổi rút các biến thế “chồng chéo” vào nhau rồi đưa về một phương trình bậc cao rất khó để chỉ ra nó có đủ 5 nghiệm. Ý tưởng đối xứng hóa ở đây cũng tương đối tự nhiên. Đây là một bài đại số ứng dụng đa thức rất mới mẻ và thú vị.
Xem lại đề bài 5 và lời giải.
Bài 6. Đây là bài hình học phẳng thứ hai của đề thi, và nó dễ hơn bài 4. Mô hình của bài toán khai thác khá mới mẻ nhưng không khó. Có nhiều cách tiếp cận để chứng minh ý b, theo kiểu tính toán hệ thức lượng hoặc biến đổi góc. Hướng xử lý theo kiểu dùng hàng điểm điều hòa như trên khá nhẹ nhàng và đẹp mắt. Nếu quan sát kỹ, ta thấy bản chất các điểm M, N chính là tiếp điểm của đường tròn bàng tiếp (A) của tam giác DEF lên các cạnh DE, DF. Ta còn chứng minh được DK, AX cùng đi qua điểm chung khác A của (I) và đường tròn đường kính AD.
Xem lại đề bài 6 và lời giải.
Bài 7. Một bài tổ hợp. Bài toán này thực ra là một cách phát biểu của khéo léo, che giấu đi bản chất vấn đề của định lý Mantel – Turan. Quan hệ “không có tam giác” phát biểu thông qua ràng buộc khá rõ, nhưng cần phải xử lý cẩn thận, vì đề cho quan hệ có hướng (trong khi định lý chỉ áp dụng được cho graph vô hướng). Trên thực tế, câu b chỉ là một cách xây dựng ví dụ cho dấu bằng xảy ra ở định lý này. Còn câu c có thể chứng minh trực tiếp bằng quy nạp.
Xem lại đề bài 7 và lời giải.
TheoLê Phúc Lữ. Người đăng: Sơn Phan.
↧
↧
Công thức nội suy Lagrange và ứng dụng - Vương Trung Dũng
Xin giới thiệu đến bạn đọc chuyên đề Công thức nội suy Lagrange và ứng dụng của thầy Vương Trung Dũng - GV PTNK TP Hồ Chí Minh. Bài viết đăng trên tạp san toán học Star Education.
Công thức nội suy Lagrange có thể dùng để:
1. Tính giá trị của một đa thức tại một điểm (cho biết giá trị tại n + 1 điểm phân biệt, tính giá trị tại điểm mới).
2. Tính tổng liên quan đến các đẳng thức tổ hợp. Chứng minh các bất đẳng thức.
3. Nội suy liên quan đến số hữu tỷ, đa thức nguyên.
Xem đầy đủ chuyên đề trong các ảnh dưới đây hoặc file PDF cuối bài.
Công thức nội suy Lagrange có thể dùng để:
1. Tính giá trị của một đa thức tại một điểm (cho biết giá trị tại n + 1 điểm phân biệt, tính giá trị tại điểm mới).
2. Tính tổng liên quan đến các đẳng thức tổ hợp. Chứng minh các bất đẳng thức.
3. Nội suy liên quan đến số hữu tỷ, đa thức nguyên.
Xem đầy đủ chuyên đề trong các ảnh dưới đây hoặc file PDF cuối bài.
File ảnh chuyên đề Công thức nội suy Lagrange
File PDF chuyên đề Công thức nội suy Lagrange
TheoStar Education. Người đăng: Tố Uyên.
↧
Đẳng thức Tổ hợp qua các bài toán Olympic - Trịnh Đào Chiến
Chuyên đề "Đẳng thức Tổ hợp qua các bài toán Olympic" của tác giả Trịnh Đào Chiến, đăng trên tạp chí toán học Epsilon 16. Xin giới thiệu cùng bạn đọc quan tâm.
Trong một số bài toán Olympic, đôi khi việc biểu diễn và tính toán liên quan đến các số tổ hợp đóng một vai trò quan trọng để tiếp tục hoàn thiện lời giải, sau khi đã có một định hướng đúng. Nhân việc trả lời thắc mắc của một số bạn học sinh về vài đoạn biến đổi của các đẳng thức tổ hợp trong tài liệu do tôi giới thiệu, bài viết này cũng rất tự nhiên được hình thành. Nội dung chủ yếu đề cập đến vai trò của những đẳng thức tổ hợp qua một số bài toán Olympic, như là sự tiếp nối để chi tiết hóa nội dung của tài liệu nêu trên mà tôi rất thích bởi hệ thống bài toán khá phong phú về Công thức nội suy Lagrange.
Trong một số bài toán Olympic, đôi khi việc biểu diễn và tính toán liên quan đến các số tổ hợp đóng một vai trò quan trọng để tiếp tục hoàn thiện lời giải, sau khi đã có một định hướng đúng. Nhân việc trả lời thắc mắc của một số bạn học sinh về vài đoạn biến đổi của các đẳng thức tổ hợp trong tài liệu do tôi giới thiệu, bài viết này cũng rất tự nhiên được hình thành. Nội dung chủ yếu đề cập đến vai trò của những đẳng thức tổ hợp qua một số bài toán Olympic, như là sự tiếp nối để chi tiết hóa nội dung của tài liệu nêu trên mà tôi rất thích bởi hệ thống bài toán khá phong phú về Công thức nội suy Lagrange.
Đầy đủ chuyên đề đẳng thức tổ hợp
File PDF đẳng thức tổ hợp qua các bài toán olympic
TheoEpsilon số 16. Người đăng: Sơn Phan.
↧
Cách giải ngắn gọn câu hệ phương trình ở đề VMO 2020
Bài viết trước đã giới thiệu 2 cách giải cho câu hệ phương trình trong đề chọn học sinh giỏi quốc gia môn Toán năm 2020 (Bài 5 - VMO 2020 - Ngày 2). Bài này giới thiệu một lời giải khác, ngắn gọn và hay hơn. Lời giải của tác giả Nhật Quang.
Xem thêm:Đề và lời giải VMO 2020: NGÀY 1 - NGÀY 2
Nhắc lại đề bài 5 VMO2020
Một lời giải khác câu 5b
TheoNhật Quang. Người đăng: Sơn Phan.
Xem thêm:Đề và lời giải VMO 2020: NGÀY 1 - NGÀY 2
↧
Giải toán Tổ hợp bằng phương pháp 'đếm bằng hai cách' - Nguyễn Tăng Vũ
Đếm bằng hai cách cho ta một phương pháp để chứng minh đẳng thức liên quan tới hệ số khai triển nhị phân hay các đẳng thức tổ hợp. Ngoài ra đếm bằng hai cách có thể áp dụng trong các bài toán bất đẳng thức, cực trị tổ hợp hay một số bài toán chứng minh sự tồn tại. Để sử dụng phương pháp đếm bằng hai cách, đòi hỏi học sinh phải biết và vận dụng tốt các phép đếm cơ bản. Bài viết này được sử dụng để giảng dạy cho học sinh lớp 10 chuyên Toán, các em mới bước đầu làm quen với các bài toán tổ hợp nói chung và các bài toán đếm nói riêng nên ví dụ được nêu ra có độ khó không cao giúp các em làm quen với phương pháp này.
Đếm bằng hai cách là một phương pháp hay gặp trong đời sống, ví dụ bài toán sau:
Một công ty nhập vào 3 xe hàng A, B, C gồm hai loại hàng I và I I. Trong đó xe A có 3 loại I và 2 loại I I, xe B có 4 loại I và 6 loại I I, xe C có 4 loại I và 6 loại I I. Tính số lượng hàng mà công ty nhâp vào.
Đây là bài toán khá đơn giản, để giải bài toán ta có thể lập bảng và khi đó ta có thể tính bằng 2 cách như sau: Tính tổng số hàng trên mỗi xe rồi cộng lại; hoặc ta có thể tính tổng số hàng loại I trên 3 xe,tổng số hàng loại 2 trên 3 xe, rồi sau đó cộng lại.
Xin giới thiệu chuyên đề nhỏ "Đếm bằng hai cách trong tổ hợp" của tác giả Nguyễn Tăng Vũ (GV PTNK HCM), đăng trên tập san toán học Star Education.
Đếm bằng hai cách là một phương pháp hay gặp trong đời sống, ví dụ bài toán sau:
Một công ty nhập vào 3 xe hàng A, B, C gồm hai loại hàng I và I I. Trong đó xe A có 3 loại I và 2 loại I I, xe B có 4 loại I và 6 loại I I, xe C có 4 loại I và 6 loại I I. Tính số lượng hàng mà công ty nhâp vào.
Đây là bài toán khá đơn giản, để giải bài toán ta có thể lập bảng và khi đó ta có thể tính bằng 2 cách như sau: Tính tổng số hàng trên mỗi xe rồi cộng lại; hoặc ta có thể tính tổng số hàng loại I trên 3 xe,tổng số hàng loại 2 trên 3 xe, rồi sau đó cộng lại.
Xin giới thiệu chuyên đề nhỏ "Đếm bằng hai cách trong tổ hợp" của tác giả Nguyễn Tăng Vũ (GV PTNK HCM), đăng trên tập san toán học Star Education.
TheoStar Education. Người đăng: Tố Uyên.
↧
↧
Một số bất đẳng thức diện tích tam giác - Trần Quang Hùng
Xin giới thiệu bài viết "Một số bất đẳng thức diện tích trong tam giác" của tác giả Trần Quang Hùng, đã được đăng trên tạp chí toán học Epsilon số 16.
Trong bài viết này chúng tôi sẽ thiết lập những bất đẳng thức về diện tích trong tam giác. Các bài toán này chủ yếu thuộc về phần các hệ thức lượng trong tam giác. Tuy nhiên chúng tôi lại giải quyết các bài toán này dựa trên một số kiến thức bất đẳng thức đại số đơn giản hoặc các kiến thức về hình học thuần túy, phù hợp với chương trình hình học cấp THCS ở Việt Nam.
Ta chú ý rằng diện tích tam giác có thứ nguyên là 2 nên việc đánh giá nó với tổng bình phương cách cạnh là đánh giá quan trọng thay vì đánh giá nó với các đại lượng khác. Các bài toán 4, bài toán 9 mới là hai mở rộng trong số rất nhiều các bài toán xoay quanh bất đẳng thức hình học kinh điển này. Xung quanh nó là vô vàn các khám phá thú vị khác đang chờ các bạn.
Trong bài viết này chúng tôi sẽ thiết lập những bất đẳng thức về diện tích trong tam giác. Các bài toán này chủ yếu thuộc về phần các hệ thức lượng trong tam giác. Tuy nhiên chúng tôi lại giải quyết các bài toán này dựa trên một số kiến thức bất đẳng thức đại số đơn giản hoặc các kiến thức về hình học thuần túy, phù hợp với chương trình hình học cấp THCS ở Việt Nam.
Ta chú ý rằng diện tích tam giác có thứ nguyên là 2 nên việc đánh giá nó với tổng bình phương cách cạnh là đánh giá quan trọng thay vì đánh giá nó với các đại lượng khác. Các bài toán 4, bài toán 9 mới là hai mở rộng trong số rất nhiều các bài toán xoay quanh bất đẳng thức hình học kinh điển này. Xung quanh nó là vô vàn các khám phá thú vị khác đang chờ các bạn.
TheoEpsilon 16. Người đăng: Sơn Phan.
↧
File PDF in lịch để bàn hình thập nhị diện đều (mặt ngũ giác)
Trang Facebook Handmade Diy Katy có tạo file để in lịch để bàn hình khối thập nhị diện đều (12 mặt đều). Mỗi mặt là một ngũ giác đều. Xin phép được giới thiệu cùng bạn đọc.
Lịch gồm 2 phiên bản: phiên bản nền trắng và phiên bản nền hoa tượng trưng cho 12 tháng trong năm. Cả 2 phiên bản đều là tiếng Việt có cả dương lịch và ngày âm lịch.
Lịch vừa dùng để xem ngày tháng, trang trí bàn làm việc, vừa có thể làm quà tặng bạn bè người thân nhân dịp năm mới. File in PDF có sẵn, các công đoạn thực hiện cực kỳ dễ. Cùng nhau tự tay làm lịch đón năm mới các bạn nhé!
Phiên bản Lịch nền trắng
Phiên bản Lịch nền hoa
File PDF để in ra giấy A4, A3: Download
Lịch gồm 2 phiên bản: phiên bản nền trắng và phiên bản nền hoa tượng trưng cho 12 tháng trong năm. Cả 2 phiên bản đều là tiếng Việt có cả dương lịch và ngày âm lịch.
 |
| Lịch để bàn hình thập nhị diện đều - Ảnh: Katy Hua |
Phiên bản Lịch nền trắng
Phiên bản Lịch nền hoa
File PDF để in ra giấy A4, A3: Download
Nguồn:Handmade Diy Katy. Người đăng: Tố Uyên.
↧
Tất tần tật về số 2020
Nhân ngày đầu năm mới 1/1/2020, bài viết này tổng hợp một số tính chất của số 2020.
2020 là một số tự nhiên chẵn gồm có 4 chữ số.
Cách đọc: Hai nghìn (ngàn) không trăm hai mươi (tiếng Anh: Two thousand and twenty).
Kí hiệu khoa học: 2.02 × 103.
Số thừa số nguyên tố phân biệt: ω(n)=3
Số thừa số nguyên tố: Ω(n)=4.
Tổng các thừa số nguyên tố: 108.
Danh sách các ước số: 1 2 4 5 10 20 101 202 404 505 1010 2020.
Tổng tất cả các ước số: σ(n)=4284.
Tổng các ước số thực sự: s(n)=2264.
Hệ thập lục phân: 0x7E4.
Hệ tam thập lục phân: 1K4.
Lập phương: 20203 = 8242408000
Căn bậc hai: 44,9444101085
Căn bậc ba: 12,6410686485
Một khối lập phương có thể tích 2020 inch-khối sẽ cao khoảng 1,1 feet.
2020 là một số Harshad bởi tổng các chữ số 2+0+2+0 = 4 là một ước của 2020.
Bạn còn biết những gì liên quan đến số 2020, vui lòng comment.
1. Cơ bản:
2020 là một số tự nhiên chẵn gồm có 4 chữ số.
Cách đọc: Hai nghìn (ngàn) không trăm hai mươi (tiếng Anh: Two thousand and twenty).
Kí hiệu khoa học: 2.02 × 103.
2. Thừa số nguyên tố:
Phân tích thành thừa số nguyên tố: 2020 = 22× 5 × 101 = 2 × 2 × 5 × 101Số thừa số nguyên tố phân biệt: ω(n)=3
Số thừa số nguyên tố: Ω(n)=4.
Tổng các thừa số nguyên tố: 108.
3. Các ước số:
Số ước số: d(n)=12.Danh sách các ước số: 1 2 4 5 10 20 101 202 404 505 1010 2020.
Tổng tất cả các ước số: σ(n)=4284.
Tổng các ước số thực sự: s(n)=2264.
4. Số giàu có:
2020 là một số giàu có, bởi tổng các ước số thực sự (2264) lớn hơn chính nó (2020).5. Trong các hệ khác:
Hệ nhị phân: 111111001002Hệ thập lục phân: 0x7E4.
Hệ tam thập lục phân: 1K4.
6. Mũ và căn thức:
Bình phương: 20202 = 4080400Lập phương: 20203 = 8242408000
Căn bậc hai: 44,9444101085
Căn bậc ba: 12,6410686485
Một khối lập phương có thể tích 2020 inch-khối sẽ cao khoảng 1,1 feet.
7. Số Harshad
2020 là một số Harshad bởi tổng các chữ số 2+0+2+0 = 4 là một ước của 2020.
Bạn còn biết những gì liên quan đến số 2020, vui lòng comment.
TheoMathVn. Người đăng: Sơn Phan.
↧