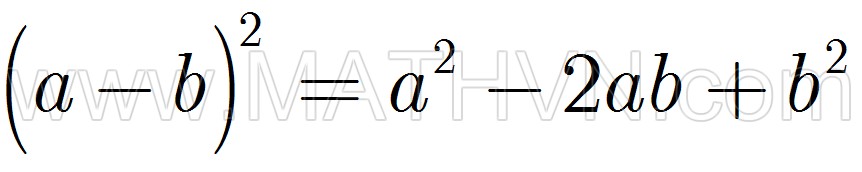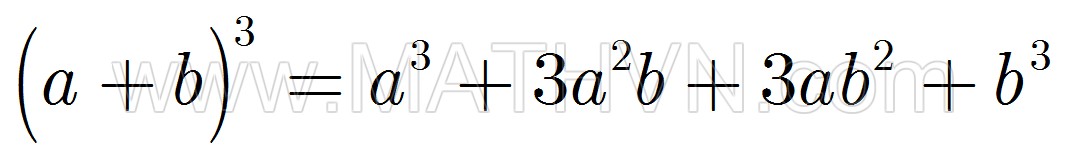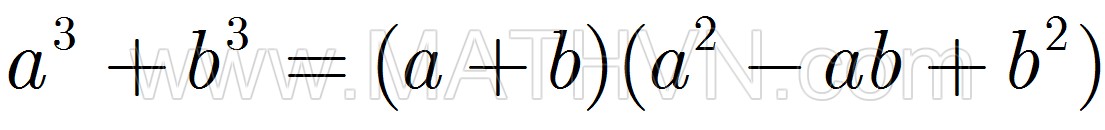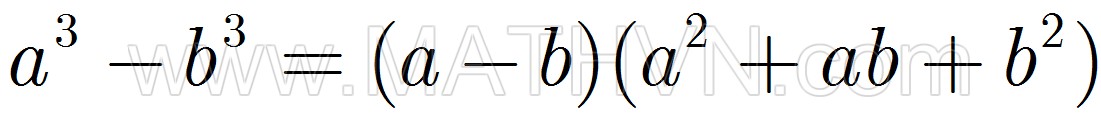Evariste Galoisđã vĩnh viễn từ giã cõi đời vào ngày 30 tháng 5 năm 1832. Những gì còn lại của chàng là tập báo cáo bổ sung lưu tại Viện Hàn Lâm Khoa học, thư gởi riêng cho người bạn thân Auguste Chevalier chàng viết đêm cuối cùng, những hồi ký viết trong tù François-Vincent Raspail còn giữ, và nhiều bút tích, kỷ vật riêng tư ở nơi Alfred Galois, người em trai của chàng. Năm 1839, Raspail cho xuất bản tác phẩm
Cải cách nhà tù: Những bức thư về các nhà tù ở Paris (
Réforme pénintentiaire: Lettres sur les prisons de Paris), trong đó Raspail công bố những gì Galois ghi chép trong tù. Hai năm sau, thi sĩ Gérard de Nerval, cùng ở tù thời gian đó với Galois, công bố bài viết “
Những nhà tù của tôi”(Mes Prisons) có kể lại chuyện phút giây giả từ cảm động với Galois khi Nerval được phóng thích.
Điều đáng nói ở đây là Alfred Galois và Auguste Chevalier không hề mệt mỏi suốt bao năm tháng đi tìm cho ra một nhà Toán học, một định chế Khoa học có thẩm quyền để xin đánh giá toàn bộ công trình Toán học mà Evariste Galois để lại. Năm 1843, tức là 11 năm sau khi Galois qua đời, họ đã thành công.
Năm ấy, Joseph Liouville 34 tuổi, một ngôi sao đang lên của làng Toán học Pháp, đang là giáo sư tại Đại học Bách Khoa Paris và đồng thời là Viện sĩ của Hàn Lâm Viện Khoa học Pháp quốc. Ông ta chưa bao giờ gặp Galois, nhưng khi người em trai của Galois tiếp cận và thỉnh cầu ông đánh giá công trình Toán học của Galois, ông nhận lời sẽ nghiên cứu và cho ý kiến về tất cả tài liệu đã được công bố cũng như chưa được công bố của Galois. Liouville là nhà Toán học đầu tiên thuộc dòng chính, đọc một cách cẩn thận và nghiêm túc công trình mà tác giả nó đã trông chờ một sự đánh giá chính thức một cách tuyệt vọng. Và Liouville vô cùng ấn tượng. Ngay năm đó, năm 1843, ông thông báo cho Viện Hàn Lâm rằng những tài liệu của Galois chứa nhiều nội dung rất quan trọng; rồi đến năm 1848, sau khi sắp xếp lại, ông cho công bố tài liệu này lên tờ tạp chí Toán học mới ra đời, tờ
Journal de Mathématiques Pures et Appliquées với tiêu đề “
Công trình Toán học của Evariste Galois” (
Oeuvres Mathématiques d’
Evariste Galois). Thật là một bất ngờ dành cho các người hâm mộ Galois. Tên tuổi và danh tiếng của người chết bắt đầu sống lại. Với dấu ấn của Liouville, người đến từ những định chế trung tâm của Khoa học nước Pháp, sự nghiệp Toán học của Galois không còn nằm trong quên lãng nữa, mà trái lại, Galois bây giờ được thế giới xem như là một nhà cách tân của Toán học.
Những ghi nhận nhẹ nhàng của Liouville khi viết phần giới thiệu “
Công trình Toán học của Evariste Galois” phần nào làm khựng lại những tình cảm nôn nóng của Chevalier và bạn bè của Galois. Liouville phê bình là Galois trình bày ý của mình quá cô đọng, thiếu triển khai cần thiết, cách diễn đạt không khúc chiết, làm các đồng Viện của ông không nắm được ý chính của những khám phá mới của tác giả. Liouville cũng gợi ý là các nhà Toán học khả kính của Viện Hàn Lâm, những người đã từng gặp trở ngại khi đọc báo cáo của Galois, “
hãy cố gắng, bằng sự sáng suốt nhất của mình, đưa ý tưởng của một thiên tài thiếu kinh nghiệm vào đúng con đường của nó”.Lời lẽ Liouville gởi tới các Viện sĩ, các nhà Toán học xem ra rất lịch sự, mang tính hòa giải; đích nhắm của Liouville trong việc biện minh cho Galois là Augustin Cauchy, vẫn là nhà Toán học và là Viện sĩ đáng kính nhất của giới Toán học và Viện Hàn Lâm. Liouville cũng không ngần ngại đề cao Galois bằng những lời tốt đẹp nhất. Ông viết: “
Nổ lực của tôi đã được đến bù xứng đáng. Sau khi lấp đầy một số khe nứt trong trong lý giải của Galois, tôi nhận ra được một nội dung và một phương pháp vô cùng độc đáo khiến cho người đồng hương của chúng ta có thể được xếp vào trong số rất ít những nhà phát minh xứng đáng nhất”(Joseph Liouville.
Oeuvres mathématiques d’Evariste Galois).
![]() |
| Joseph Liouville (1808-1882) |
Sự hỗ trợ sủa Liouville là bước ngoặc của sự nổi tiếng của Galois sau khi Galois qua đời. Qua vài thập niên sau, công trình của Galois từ từ thấm vào dòng chính của Toán học thế kỷ 19, đỉnh điểm là Camille Jordan với tác phẩm
Traité des substitutions xuất bản năm 1870 (René Taton.
Dictionary of Scientific Biography, vol.5). Nhưng điều có ý nghĩa là câu chuyện của Galois đã di chuyển từ những chuyện bên lề lịch sử nói về những nhóm người quá khích trong Cách mạng Pháp, chuyển sang câu chuyện khám phá Toán học đang được các định chế Khoa học đánh giá cao. Năm 1848, hai năm sau khi Liouville đã công bố báo cáo về Galois, vẫn còn những bài báo nói về những chuyện bên lề của các nhóm quá khích, trong đó có vai trò của Evariste Galois, thí dụ như bài báo trong tạp chí
Magasin Pittoresque (n.16, 1848). Tuy nhiên, những bài báo loại này dần dần nhường chỗ cho những bài nhận định đứng đắn về nội dung Toán học do của các nhà Toán học uy tín thời ấy viết. Có một chút mỉa mai là người ta thấy huyền thoại về Galois được đề cao ngay ở những nơi trước đây đã từng lạnh nhạt với chàng (Viện Hàn Lâm), hoặc đã loại chàng ra khỏi định chế ấy (trường Sư Phạm đã đuổi học Galois ngay năm thứ nhất của chàng ở trường này).
Năm 1895
trường Cao Đẳng Sư Phạm (
École Normale Supérieure, ENS, tên mới của trường Sư Phạm kể từ 1845, làm lễ kỷ niệm 100 năm ngày thành lập trường. Nhân dịp ấy trường có ra một tập kỷ yếu mang tên
Le centenaire de l’ École Normale (Trường Sư Phạm trăm tuổi), trong đó có phần ghi lại tên tuổi và ảnh hưởng việc làm của các cựu học sinh nổi tiếng của trường (Chú thích của người viết: Những người đang học ở các Trường Lớn hoặc đã tốt nghiệp như trường Bách Khoa, trường Sư Phạm,…đều tự gọi mình là
học sinh họăc
cựu học sinh). Chủ nhiệm tập kỷ yếu có nhờ một nhà Toán học ngoại quốc (Na Uy) tên là Sophus Lie (1842-1899) viết về Evariste Galois. Lý do là vì Lie là người ngoại quốc hiếm hoi thời ấy đã có những công trình nghiên cứu về Galois, và cũng chính Lie là người đã dùng câu chữ
Théorie de Galois (Lý thuyết Galois) đầu tiên. Trong bài dài 9 trang của Sophus Lie đăng trong tờ kỷ yếu, mang tiêu đề
Influence de Galois sur le développement des Mathématiques (Ảnh hưởng của Galois trên sự phát triển Toán học), Lie nhấn mạnh đến những ảnh hưởng sâu sắc của những gì Galois đã tìm ra trên sự phát triển của Toán học sau hơn 60 năm ngày mất của Galois. Tòa soạn kỷ yếu cũng nhờ nhà Sử học Paul Dupuy (1856-1948) viết tiểu sử của Galois để ghi lại những gì xảy ra và những gì Galois đã làm được trong cuộc đời ngắn ngủi của chàng. Bài viết này đi kèm với bài viết của Sophus Lie tạo thành một tập tài liệu đáng tin cậy cho các thế hệ sau khi muốn tìm hiểu về Galois. Tưởng cũng cần nói thêm một chi tiết thú vị là nhà sử học Paul Dupuy ngày ấy là Tổng giám thị của trường ENS, người có vai vế thứ nhì trong việc gìn giử kỹ luật của trường (sau Hiệu trưởng), nay được phân công viết tiểu sử cho một học sinh của trường bị đuổi học vì lý do kỷ luật 65 năm trước!
![]() |
| Paul Dupuy (1856-1848) |
![]() |
| Sophus Lie (1842-1899) |
Dupuy làm công việc được giao một cách nghiêm chỉnh. Ông tập hợp tất cả những bài được công bố, chưa được công bố của Galois, ông lùng sục các kho tài liệu lưu trữ ở trường Cao Đẳng Sư Phạm, ở Viện Hàn Lâm, ở Bộ Giáo Dục, và cả những bệnh án, báo cáo tử của bệnh viện nơi Galois chết. Ngoài ra ông còn vào tìm những hồ sơ tù nhân lưu trữ ở nhà tù Sainte Pélagie nữa. Rồi ông tiếp xúc những người còn sống bà con với Galois để nghe kể về những chuyện bên lề cuộc sống của Galois. Lúc đầu Paul Dupuy chỉ dự trù viết một bài báo về tiểu sử của Galois đáp ứng yêu cầu của tòa soạn tập kỷ yếu của trường ENS, nhưng sau này nó trở thành một cuốn sách tiểu sử đầy đủ của Evariste Galois, xuất bản năm 1848 mang tựa đề
La Vie d’ Evariste Galois (Đời sống của Evariste Galois). Cuốn sách này được coi như một số đặc biệt của tờ
Annales scientifiques de l’École Normale Supérieure. Vì Dupuy là một nhà sử học, không phải là một nhà Toán học, lại là một người phụ trách về kỹ luật của một Trường Lớn, cho nên trong cuốn tiểu sử của Galois không có chỗ cho tình cảm và cũng không có chỗ cho những ý kiến thiên lệch chủ quan.
Khi được hỏi về nguyên do cuộc sống quá nhiều sóng gió của Galois, Dupuy có cùng ý nghĩ với những người “Cộng hòa” khi cho rằng Galois đã sống như một người xa lạ bên cạnh những người khác mà chàng gọi là “chiến hữu”. Dupuy nói thêm: “
Xứ sở của chàng, xứ sở tuyệt vời của chàng phải là xứ thật rộng, thật đẹp, ở đó mọi người thật thông minh đắm chìm trong chân lý chính xác của Toán học”(Dupuy.
La Vie d’Evariste Galois, p.252). Nói cách khác, thế giới của Galois phải rất trong sáng, rất hữu lý, một thế giới lý tưởng thuần khiết. Bị đày xuống sống chung với chúng ta trong một thế giới nhiều thay đổi và đầy biến động, hoặc Galois phải cam chịu, hoặc Galois nổi loạn. Nếu Galois thi đậu vào trường Bách Khoa thì chàng đã gục ngã trước hàng rào ngăn chặn trong cuộc biểu tình bạo loạn tháng 7 năm 1830. Nếu Galois tránh được trận tử chiến tay đôi trong buổi bình minh hôm ấy thì sao? Thì chàng cũng sẽ chết dưới họng súng của lực lượng đàn áp bạo loạn của triều đình trong ngày biến động tháng 6 năm 1832. Cũng theo Dupuy thì khi lạc vào thế giới đầy bất trắc của chúng ta, con người xa lạ ấy đã bị thần chết chọn lựa chỉ cho sống một thời gian ngắn thôi.
Trong khoảng thời gian trường Cao Đẳng Sư Phạm đang ôm ấp đứa học trò “lạc loài” của mình thì một định chế khác cũng ca tụng vinh danh một người mà đã một lần bị từ chối. Năm 1897, một năm sau khi cuốn tiểu sử của Paul Dupuy viết về Galois ra đời, hội Toán học Pháp quốc (La Société Mathématique de France) cho tái bản tác phẩm
Oeuvres Mathématiques d’
Evariste Galois do Liouville xuất bản lần đầu cách đây 50 năm. Lần tái bản này có kèm theo lời giới thiệu tác phẩm của Galois do Émile Picard, Viện sĩ Viện Hàn Lâm, đại diện cho hội Toán học Pháp quốc, viết. Trong lời giới thiệu ấy có đoạn viết:
Tuy đời sống của thiên tài quá ngắn và có quá nhiều đau khổ nhưng Galois đã để lại cho Khoa học một dấu ấn thật sâu đậm. Những bộ óc thông minh sắc bén không phải là hiếm có trong số các nhà Toán học của chúng ta, nhưng Galois là một trong những bộ óc nổi trội nhất. Than ôi, hình như chàng tuổi trẻ của chúng ta phải trả món nợ đáng buồn cho cái thiên tài của mình!
Auguste Chevalier, người bạn thân của Galois, trong bài điếu văn cũng có nói: “
Galois đã chết sớm vì cái thiên tài của mình”.
![]() |
Tác phẩm Oeuvres Mathématiques d’ Evariste Galoisvới lời giới thiệu của Émile Picard. |
Jules Tannery (1848-1910), nhà Sử học và cũng là giáo sư Toán tại trường Cao Đẳng Sư Phạm, 10 năm sau ngày tác phẩm trên được tái bản, đã cho tái bản lần thứ ba tác phẩm ấy. Trong lần tái bản mới này, Tannery có bổ sung những tài liệu của Galois chưa hề được công bố. Rồi năm 1909 một tấm bảng lưu niệm được cho gắn tại nơi sinh của Galois ở Bourg-la-Reine, trong buổi lễ ấy Tannery là diễn giả. Ông nói rằng Galois đã đem tài năng của mình để khám phá một lãnh vực trừu tượng của một bộ môn trừu tượng nhất của Khoa học: Toán học.
![]() |
Plaque commémorative Evariste Galois 54, Avenue du Général-Leclerc, Bourg-la-Reine, France (Ảnh chụp do người viết sưu tầm. Dịch: Ở đây là nhà của E.Galois, nhà Toán học thiên tài) |
Cho tới thời gian này, câu chuyện về nhà Toán học thiên tài vắn số vẫn tiếp tục được lan rộng. Nó đã thấm vào những sinh hoạt khoa học và chính trị của các định chế ở Paris rồi tạo thành huyền thoại cho thế giới Toán học. Trong giai đoạn đầu thì huyền thoại này chỉ có ở nước Pháp, từ ngày có những bản dịch sang tiếng Anh, huyền thoại này truyền ra khắp thế giới. Hai người đóng vai chính của sự biến đổi Galois từ một anh hùng của nước Pháp thành biểu tượng Toán học của cả thế giới là George Sarton (1884-1956) và Eric Temple Bell (1883-1960).
Sarton sinh đẻ ở Bỉ năm 1884, di cư sang Mỹ từ năm 1915 khi quê hương ông bị Đức xâm chiếm. Mặc dù được đào tạo để trở thành một giáo sư Toán, nhưng Sarton lại ưa thích môn Lịch sử Khoa học, và sau đó được mọi người biết tới như là một trong những nhà viết sử Khoa học chuyên nghiệp. Sarton rất quen biết câu chuyện về Galois từ ngày ông còn là sinh viên Toán ở Ghent. Rồi sau này ông có ý định đem câu chuyện bi thảm này trình bày trước công chúng Mỹ. Năm 1921 ông công bố một tiểu sử ngắn của Galois trên tạp chí
Scientific Monthly, sau đó bổ sung và cho in lại nhiều lần trong những năm kế tiếp, cuối cùng năm 1937 một bản tiểu sử đầy đủ của Galois được xuất hiện trong tạp chí riêng của ông, tờ
Osiris.![]() |
| Eric Temple Bell (1883-1960) |
![]() |
| George Sarton (1884-1956) |
Cuốn tiểu sử Galois của Sarton dựa trên cuốn nghiên cứu của Dupuy. Nếu Dupuy quan tâm đến con người Galois, tìm cách tái tạo con người Galois và mang Galois về với nền Khoa học Pháp, thì Sarton đưa Galois lên thành mô hình một thiên tài Toán học trẻ tầm vóc thế giới. Theo Sarton, Galois là một ông Thánh, không phải tử vì đạo mà tử vì Khoa học. Sarton viết: “
Ngọn lửa trí óc của Galois sẽ còn cháy qua nhiều thế hệ, đó là nguồn sáng tạo vĩnh viễn”. Sarton phân biệt
tài năng và
thiên tài thật sự. Rõ ràng là thành quả to lớn của một con người trẻ trong một khoảng thời gian rất ngắn không thể là kết quả của một tài năng thông thường, mà đó là ánh chớp sáng rực của một thiên tài thực sự. Sarton viết: “
Nếu thành quả to lớn diễn ra từ từ,chầm chậm, thì không thể phân biệt được tài năng và thiên tài, nhưng nếu nó nổ bùng sáng lóe lên thì rõ ràng là có sự hiện diện của một cái gì đó thiêng liêng trên hẵn tài năng thông thường”.(Sarton
. Evariste Galois, p.256). Nhưng bất hạnh thay, vẫn theo Sarton, sự bùng sáng của thiên tài ấy phải trả bằng một giá quá nặng. Chúng ta đã có một bài học quá đen tối từ cuộc sống ngắn ngủi của Galois. Sarton viết: “
Nếu Galois đơn giản chỉ là một nhà Toán học có tài, có thể đời sống của Galois ít bi thảm hơn, ông có thể dùng tài năng Toán học của mình để thăng tiến, và có một cuộc sống hạnh phúc. Đằng này không phải vậy, sự điên cuồng Toán học đã ám ông và ông không có chọn lựa nào khác là đầu hàng số mệnh”. (Sarton
. Evariste Galois, p.256).
Sự việc Evariste Galois trở thành biểu tượng cho Toán học trên toàn thế giới được hoàn tất bởi Eric Temple Bell. Chương tiểu sử của Galois trong tác phẩm
Men of Mathematics do Bell viết, xuất bản năm 1937, nổi tiếng đến nổi tác phẩm của Bell trở thành sách bán chạy nhất (The best seller). Eric Temple Bell là một nhà Toán học giảng dạy tại California Institut of Technology (C.I.T), đồng thời cũng là văn sĩ viết truyện Khoa học giả tưởng dưới tên là John Taine. Ước vọng của Bell là được biết dưới danh hiệu là văn sĩ. Tác phẩm về tiểu sử nổi tiếng đã trở thành cổ điển, cuốn
Men of Mathematics, cho thấy ông vừa có kiến thức Toán học rộng và vững chắc, lại vừa có căn bản và tham vọng văn chương. Trong lời giới thiệu cuốn sách ấy, nhà Sử học Davis Eugene Smith có viết: “
Tác giả cuốn sách này là một văn sĩ nhưng được mọi người biết tới như là một nhà Khoa học, và ông cũng là một nhà Khoa học viết sách như một văn sĩ”.
“
Thiên tài và sự Ngu dốt” (
Genius andStupidity) là tựa đề Bell dành cho phần viết vể Galois. Ngay ở phần mở đầu, tác giả nói ngay luận điểm của mình: “
Trong lịch sử của Khoa học, không có thí dụ nào đầy đủ nói lên chiến thắng của sự ngu dốt đối với thiên tài, hơn là những gì được thấy qua cuộc đời quá ngắn ngủi của Evariste Galois.”(Bell.
Men of Mathematics, p.362). Trong phần còn lại của bài viết, Bell kể lại câu chuyện đời đầy buồn đau của Galois và những người “điên” đi qua cuộc đời chàng. Đầu tiên là những thầy giáo của trường Louis-le-Grand. Theo Bell, “
đó là những người tốt, kiên nhẫn, nhưng họ là những người ngu dốt”. (Bell.
Men of Mathematics, p.365). Những người kế tiếp trong danh sách những người “điên” là những giám khảo của trường Bách Khoa, ông Hiệu trưởng Guigniault, cảnh sát “chìm” ở Paris, và giới chức ở nhà tù Sainte-Pélagie. Bell không xếp những ông Viện sĩ Cauchy và Poisson vào chung vào danh sách nói trên, nhưng thực ra là ông rất muốn. Bell nói: “
Sức mạnh của Galois bị tan vỡ trước một đám “điên”, chúng liên tục chống lại chàng khiến cho, trong suốt cuộc sống, chàng phải đánh trả hết thằng này tới thằng khác”.(Bell.
Men of Mathematics, p.362).
Ấn tượng sâu đậm lưu lại trong trí óc sau khi đọc tiểu sử của Galois do Bell viết, là nguồn cảm hứng của một số nhà Toán học và Vật lý học nổi tiếng của các bộ môn ấy, chẳng hạn như Leopold Feld (1898-1968), James Newman (1907-1966), Fred Hoyle (1915-2001), John Nash (1928-2015), Freeman Dyson (1923-).
Tất cả những người này đều nói rằng tiểu sử của Galois do Bell viết có ảnh hưởng rất lớn trong cuộc sống và sự chọn lựa nghề nghiệp của họ. Câu chuyện về Galois của Bell được lặp đi lặp lại trong các lớp Toán bởi các giáo sư, được trích dẫn trong sách Toán ở nước này nước khác, Galois trở thành biểu tượng của một thiên tài Toán học hiếm có trong lịch sử Khoa học trên toàn thế giới.
Tác giả bài viết:Anh Le, Ph.D (Hoa Kỳ)
Email: leqanh36 [dot] gmail.com
Được đăng trên www.MathVn.com
Xem thêm:Galois - Phần 1 / Galois - Phần 2 - Phần 3